Binary Tree: Lowest Common Ancestor (LCA)

Module: Binary Tree

You can refer to the Leetcode problem 236. Lowest Common Ancestor of a Binary Tree

Problem Statement

Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

Example 1:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3
Explanation: The LCA of nodes 5 and 1 is 3.

Example 2:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
Output: 5
Explanation: The LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.

Intuition

We need to find the common first parent which has both p and q as descendants.

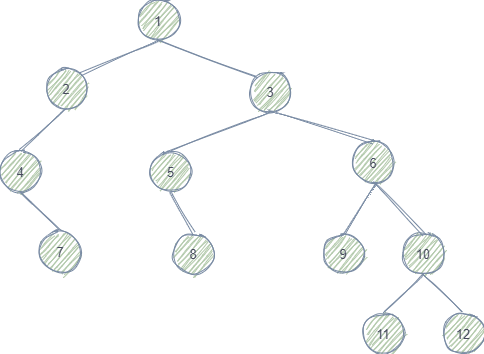
Consider the following Binary Tree:

Input: root: [1, 2, 3, 4, null, 5, 6, null, 7, null, 8, 9, 10, null, null, null, null,null, null, 11, 12]
p: 8
q : 11

• We can follow the recursive pre-order dfs traversal and go on comparing the current node with p and q.

if(root == null ){
  return null;
}

• For each/any given node(root), check:
  1. If root is null, then we return null.
  2. If the one of the nodes among p and q is root itself? It means we found a match and in that case, we need to return that node, the matched root.

So for this we can compare the the root with both p and q.

if(root == p || root == q){
  return root;
}

• If any of the target nodes p/q does not exist in left child, it will be null. And similarly for right child, it will be null.

• Once a match is found in either left or right subtree, it is returned back(upward) to the recursive call and then compared with counter part (left or right value). If both the values are found, let say p is found in left subtree and q found in the right subtree, then the current root, parent of left and right is returned as lca.

• If none found, null will be returned.

• Follow the blue arrows, when 8 is found(from lca(root.right, 8, 11) of root node 5), it is compared with left child null and 8 is returned from the call stack of root 5.

• Similarly, node 11 gets returned as a result of recursive call from root 3.

• Finally, in the call stack of root node 3, left node is 8 and right node is 11. These 2 values are compared and since both are present(not null), current root (3) is returned which returned back till Tree root 1.

Complexity Analysis

Time complexity: O(N), where N is the number of nodes in the binary tree. In the worst case(left skewed or right skewed) we might be visiting all the nodes of the binary tree.

Space complexity: O(N). This is because the maximum amount of space utilized by the recursion stack would be N since the height of a skewed binary tree could be N.

program

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {

        if(root == null){
            return null;
        }

        if( root == p || root == q){
            return root;
        }

        TreeNode lNode = lowestCommonAncestor(root.left, p, q);
        TreeNode rNode = lowestCommonAncestor(root.right, p, q);

        if(lNode == null)
            return rNode;

        if(rNode == null)
            return lNode;

        return root;
    }
}

Test cases

[3,5,1,6,2,0,8,null,null,7,4]
5
1
[3,5,1,6,2,0,8,null,null,7,4]
5
4
[1,2]
1
2

Related problems

• Lowest Common Ancestor of a Binary Tree II
• Lowest Common Ancestor of a Binary Tree III
• Lowest Common Ancestor of a Binary Tree IV

Problem Credit : leetcode.com